By Wyatt Benno — Apr 4, 2024

The cost of composition: an exploration in the state of the art for foreign field arithmetic in zero knowledge proofs.

'Foreign field' or 'non-native field' arithmetic appears everywhere in zero knowledge proof systems. If you want to use ZKP for boolean operations, public-key cryptography, or proof composition you will undoubtedly run into the constraint blowup due to foreign field work. However, if you look into open-sourced code repo such as Arkworks — you will notice that the way developers generally deal with this has not been updated in a while. People often say, 'we can use composition to get XYZ proof system on constrained L1 (ETH)', but without creating novel and often highly creative methods for dealing with 'non-native field' arithmetic, this is not practical. In fact, protocols often take large hits in gas fees because they cannot figure out more optimal proof composition. So what are foreign fields and what is the state of the art for dealing with them?

Foreign field arithmetic refers to performing operations on elements that belong to a finite field different from the native finite field of the zero-knowledge proof system. Read this Wiki article to catchup on what a finite field is. For example, a ZKP system might use a large prime field (Fp) for its native operations, but need to prove statements about elements in another prime field (Fq). The challenge arises because representing foreign field elements from Fq in Fp is very expensive in terms of the number of constraints required.

The inefficiency of foreign field arithmetic is a major bottleneck for the practical scalability and cost of zero-knowledge proof systems, especially for applications that inherently require operating in multiple fields, such as proof composition. Proof composition involves verifying proofs that themselves verify other proofs, requiring "nesting" of operations in different fields. For example, getting a proof system such as Nova or Lasso into a Groth16 wrapper for on-chain verification. Or using a Lasso proof in another proving scheme that may have better memory efficiency (Nova).

Let's try once for Lasso/JOLT.

We can attempt proof composition by running Lasso over the Grumpkin curve and composing with Groth16. This means turning the whole Lasso verifier into a circuit over the BN254 scalar field. Lasso has a few steps involved with verification one of these is a polynomial commitment scheme (PCS). The current repo uses the Hyrax PCS. The Hyrax verifier does two MSMs over the Grumpkin base field — which equals the BN254 scalar field.

In the context of the Grumpkin elliptic curve used in circuit, the scalar field is Fr, while the base field of the curve is Fq. Circuits normally work in the scalar field. Multi-scalar multiplication (MSM) involves computing a linear combination of elliptic curve points, where the scalars are Fr elements, and the points are Projective elements (which have coordinates in Fq / also called the base field of the curve). With Arkworks you can do this work in circuit with NonNativeFieldVar which has some optimization.. but will still result in millions of constraints. Around a 500x overhead!

Then after that the circuit will need to do the sum-check verifier's work with potentially non-native arithmetic (the sum-check verifier in Lasso/Jolt will be working over the Grumpkin scalar field, which is the BN254 base field). Doing this naively, once again leads to constraint blow-up.

*Testudo is a common code repo people refer to for seeing how this would work. The project was stopped before the PCS was done, but they did do sum-check in circuit.

So what to do?

Many suggest switching to PCS that have logarithmic verifier costs such as HyperKZG or Zeromorph. This will indeed help get the verifier into a state that will cost less in 'gas' fees. In some cases the L1 will even have precompiles ready for specific PCS. However, this side-stepping is still not optimal as other parts of the verifier circuit will continue to use non-native field work as shown above. Even if researchers go to great lengths to eliminate them, such as in CycleFold, there is still a cost when trying to get the verifier 'on-chain'. Which means ultimately, we will need to face non-native field work in some way or form! 👻

What is the state of the art in the literature?🤺

The most recent work is a paper titled: "Beyond the circuit: How to Minimize Foreign Arithmetic in ZKP Circuits". In this work the authors introduce three new concepts dealing with foreign field work.

A protocol for proving equality of discrete logarithms across different groups (i.e. with different prime orders) using rejection sampling. This avoids having to embed foreign group arithmetic in the proof statement.
A Σ-protocol that allows performing elliptic curve scalar multiplication outside the circuit and binding it to the circuit with a hash function. This avoids expensive non-native field arithmetic inside the circuit. Hash functions such as Poseidon work very efficiently in circuit.
Lastly they give an algorithm for proving knowledge of an AES encryption using a single lookup argument, avoiding the need for boolean arithmetic in the circuit.

The second Σ-protocol is a surprisingly straight forward way to delegate the hard work to the prover and let the circuit simply use a hash.

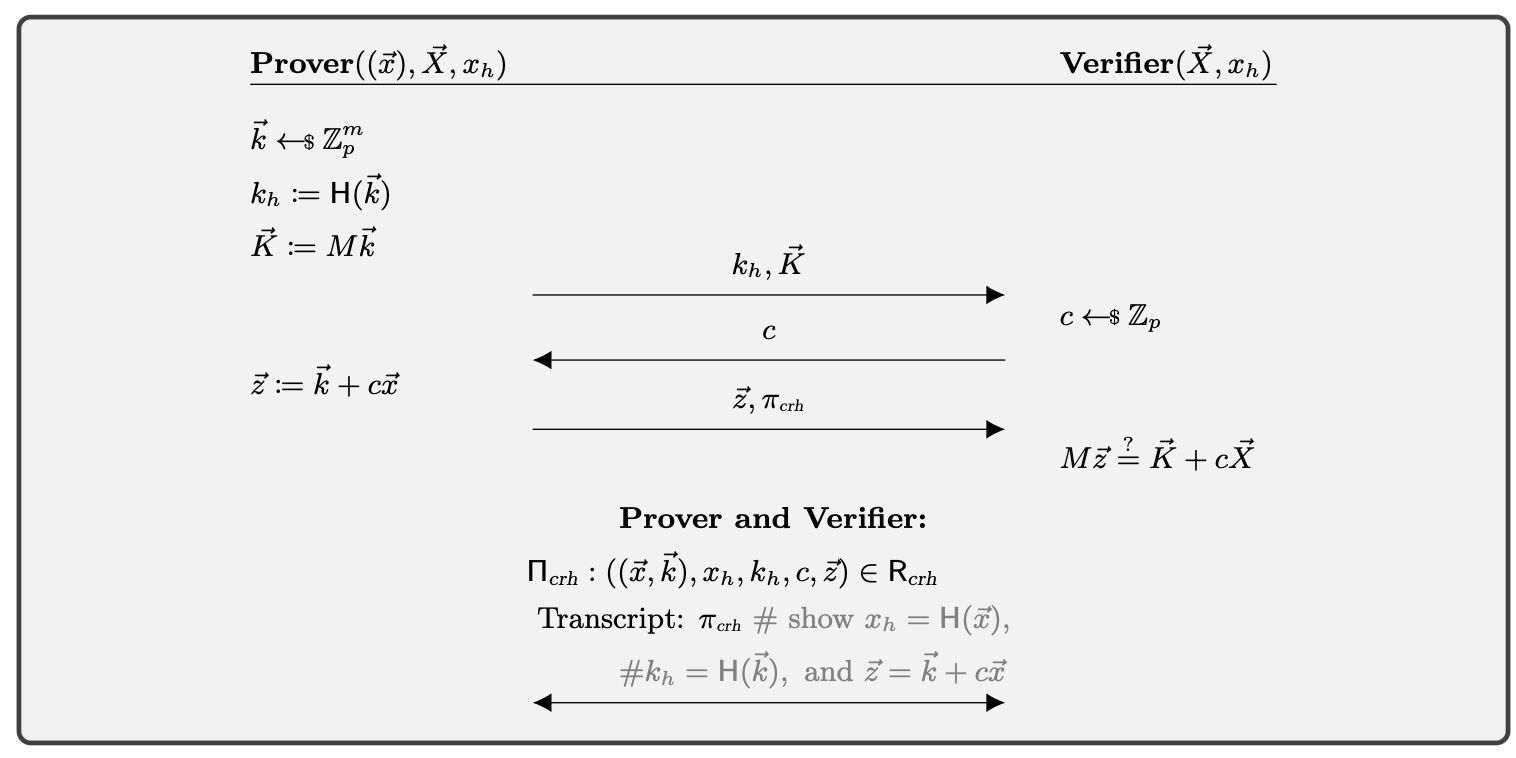
In this case, non-native work is avoided in the circuit, but then the verifier still needs to do the checks. If these are curve points this is not likely to be a problem, but in the more general cases, for example something like a matrix-vector product, or MSM, the constrained L1 verifier may be too expensive to be useful in practice.

Is there a way to remove foreign fields from the circuit while keeping verifier costs low?

If we can use the tricks from SigmaKit with other techniques we can create generalized techniques (SigmaSuite) where both circuit and verifier costs are low. This would become a state of the art technique for handling foreign field arithmetic in proof composition.

There are a few possible directions to go with this. For example doing the Σ-protocol technique multiple times to move work outside of the circuit and allow for a simpler verifier. A problem appears on the second step as we are now hashing large vectors in circuit. Maybe we can deal with these via Merkle trees or chains of hashes? The issue then becomes potentially large costs once again in the verifier.

The Testudo work showed that sum-check to Groth16 in R1Cs is practically possible. We propose using SigmaKit's Σ-protocol to remove non-native field arithmetic from the circuit, with a combination of the sum-check protocol. An in-circuit sum-check verifier can be used for checking of equalities and creating a final compressed proof (Groth16); these checks would otherwise be done by the verifier contract 😬. Moreover, if using Groth16 the proofs can be aggregated with SnarkPack or other methods. The combination of these techniques will result in performant circuits for proof composition (with no non-native field work) that still have succinct proofs for on-chain verifiers.

We look forward to contributing to an open source suite of these tools for various non-native field arithmetic tasks. The ideas from Sigmabus (SigmaSuite) can be added to projects like Arkworks or Bellperson and used by all 🙌.

*Thank you SuccinctJT for previous conversations on the subject of proof composition in Lasso. Thanks Arnaucube for iterations and discussion on implementations of a generalized SigmaKit.

Let's try once for Lasso/JOLT.

So what to do?

Is there a way to remove foreign fields from the circuit while keeping verifier costs low?

Subscribe to ICME